Интерполяция - метод нахождения промежуточных переменных функции по нескольким уже известным значениям. Впервые формулировка "интерполирование" была введена Джоном Валлисом в научном сочинении "Арифметика бесконечных".
Линейная интерполяция
Простейшим случаем интерполяции является "линейная", то есть нахождение величины по двум заданным точкам. Данный процесс вычисления можно рассмотреть как линейную функцию, тем самым делая расчёт более наглядным. Нанесение функции на систему координат называют аппроксимацией. Для этого на оси координат необходимо провести прямую через известные точки. Логично, что искомое значение, находящееся между первыми двумя точками, можно найти графически, зная абсциссу X. Если координата X искомой величины лежит за пределами известных значений (X1, X2), то процесс вычисления называется экстраполяция.
Калькулятор позволяет определить значение ординаты Y искомого значения, зная координаты X и Y двух других функций, а также её абсциссу. Для вычисления необходимо ввести значения заданных двух точек Х1, Y1 и X2,Y2, а также указать координату X искомой точки, а сервис автоматически определит метод расчёта и произведёт его.
Формула линейной интерполяции
Для вычисления используется следующая формула:
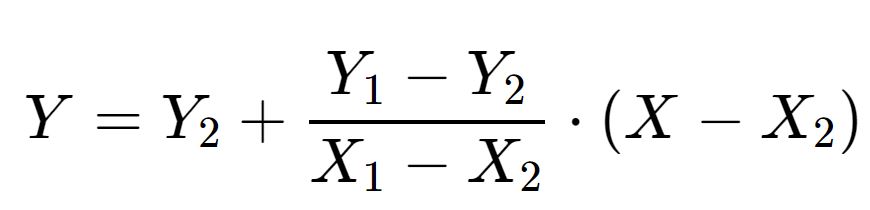
Пример расчёта
Дано: координаты двух точек А(3;1.5) и B(6;5).
Найти: ординату точки С с абсциссой 4.5.
Для удобства рекомендуется построить график: нанести точки на систему координат и провести прямую.
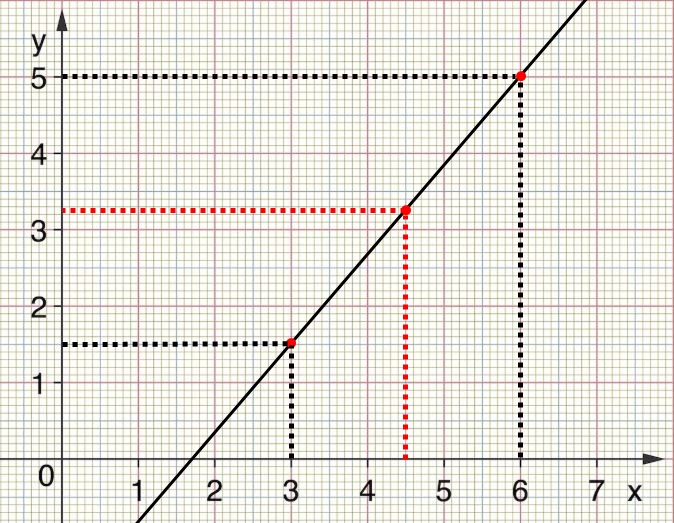
После этого подставляем значения в указанную формулу:
Y = 5 + (1.5 - 5) / (3 - 6) · (4.5 - 6) = 5 + (-3.5) / (-3) · (-1.5) = 3.25.

Добавить комментарий